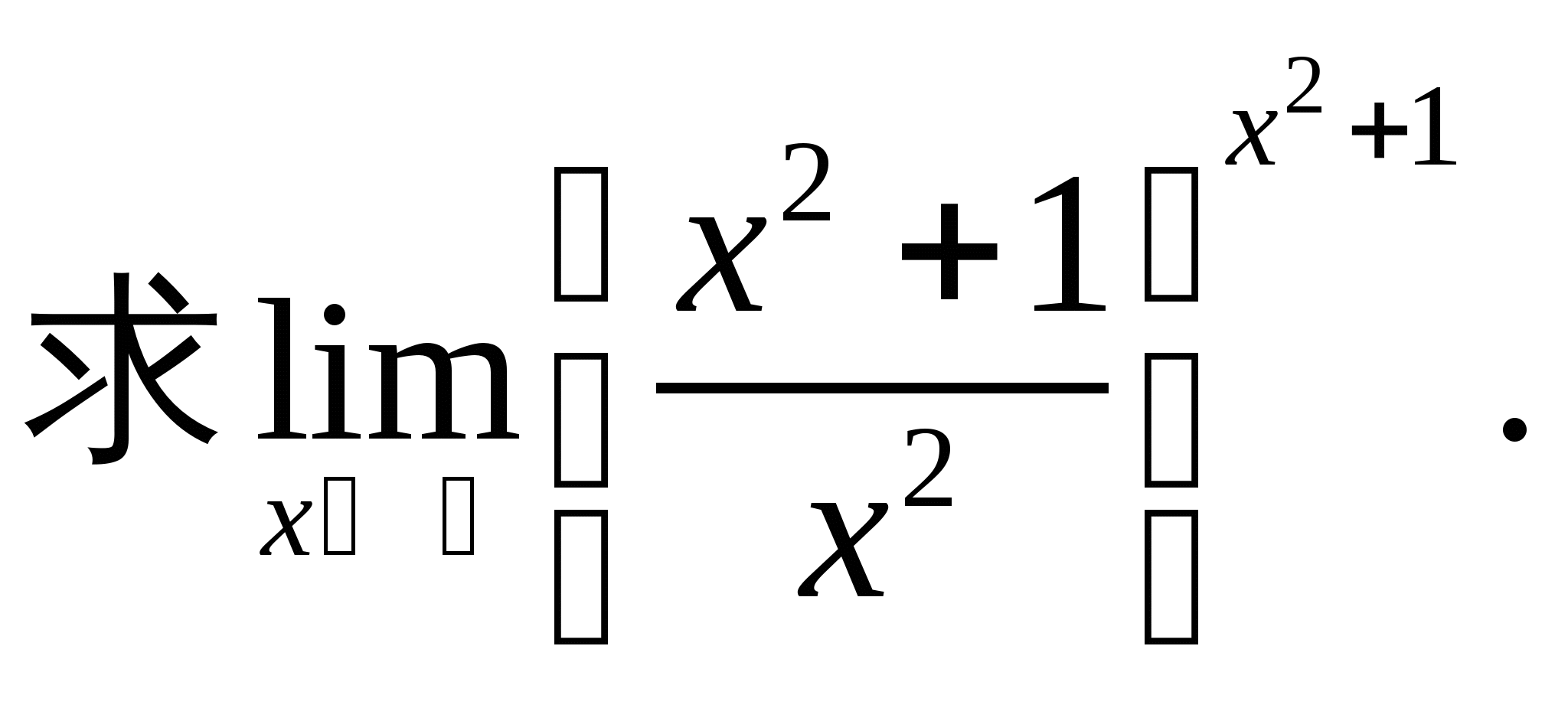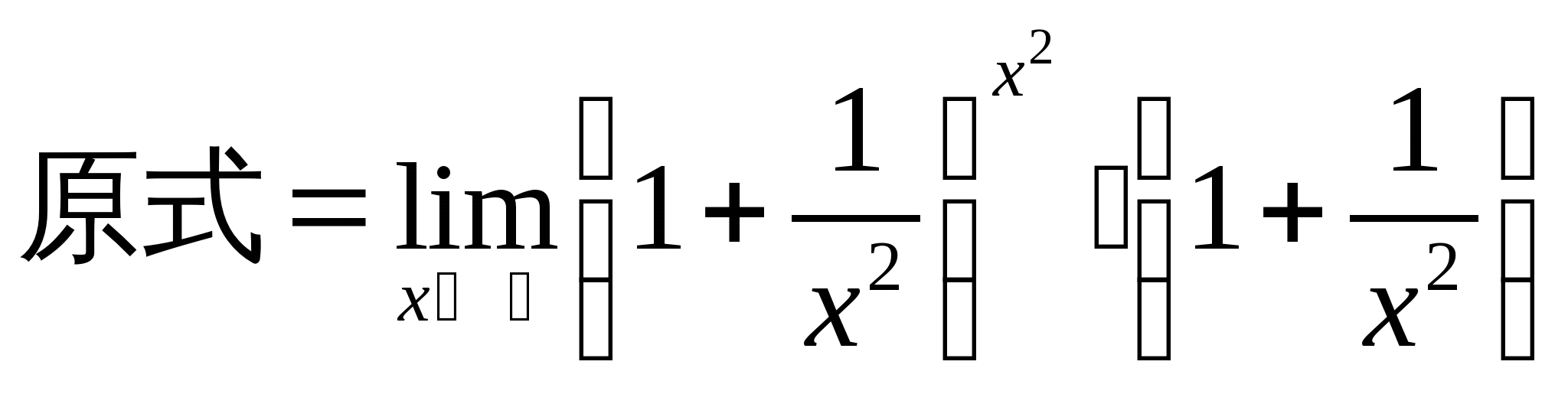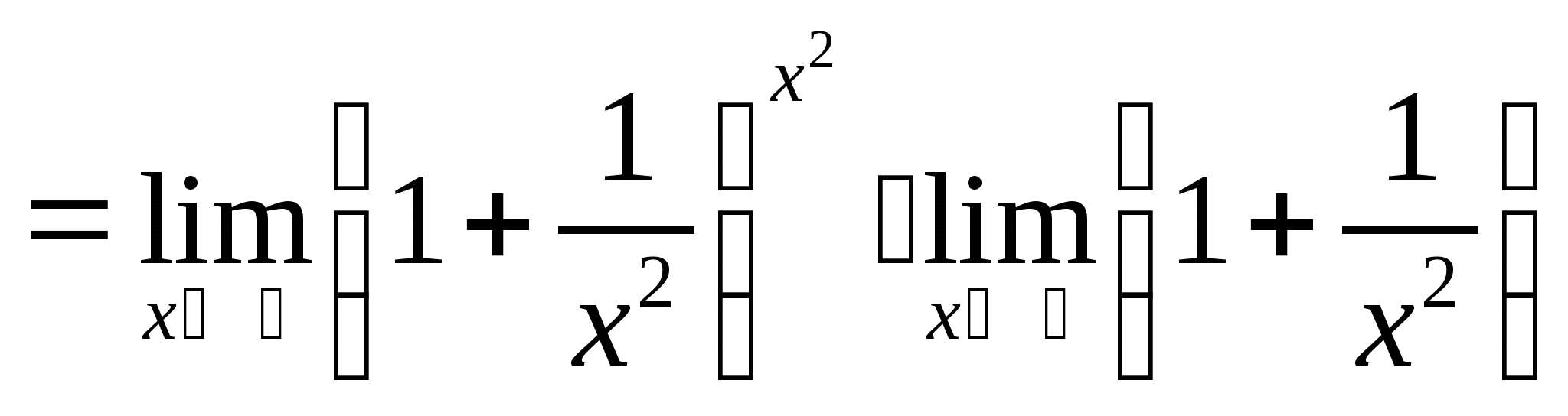安徽财经大学商学院《微积分》课程讲稿
内容 (标题) | 两个重要极限 | 课时 | 1学时 |
教学目的及要求 | 教学目的:
具体要求:
| ||
重点难点及其处理 | 重点 两个重要极限; 两个重要极限的应用 难点 两个重要极限的证明 | ||
教学方法 | 采用“提纲式”或“问答式”讲授,启发诱导; 多讲解习题巩固新知识,讲练结合 | ||
教学过程 | 两个重要极限 一、重要极限Ⅰ
证明:在单位圆内,设圆心角 ∠AOB ⊿AOB的面积 < 扇形AOB的面积 <⊿AOD的面积 而 ⊿AOB的面积
既有
因此, 于是,由夹逼定理得
又由于
因左右极限均存在且相等,故有
| ||
教学过程 | 注意:当 该极限也可表示为: 其中 例1. 求 解:
例2. 求 解: 例3.求 解: 例4.求 解: | ||
教学过程 | 二、重要极限Ⅱ
证明思路:对于数列
可以证明, 对于
又由于
当
对于
综上可得
| ||
教学过程 | 注:1若令
2该极限属于
其中当
其中当 这个重要极限应灵活的记为:“以1加非零无穷小为底,指数是无穷小的倒数,其极限为数e”. 例5. 解:
例6.求 解: 例7.求 解: 例8.求 解: 例9. | ||
教学过程 | 解:
课堂练习: 解:
三、小结 两个重要极限
| ||
参考文献 | 1.《微积分》,龚德恩等,四川人民出版社,1999年。 2.《微积分》. 李天胜主编. 电子科技大学出版社,2002年8月版 3.《微积分同步练习与模拟试题》(配套练习) | ||
课外作业 | 课后习题 | ||
后记 | |||

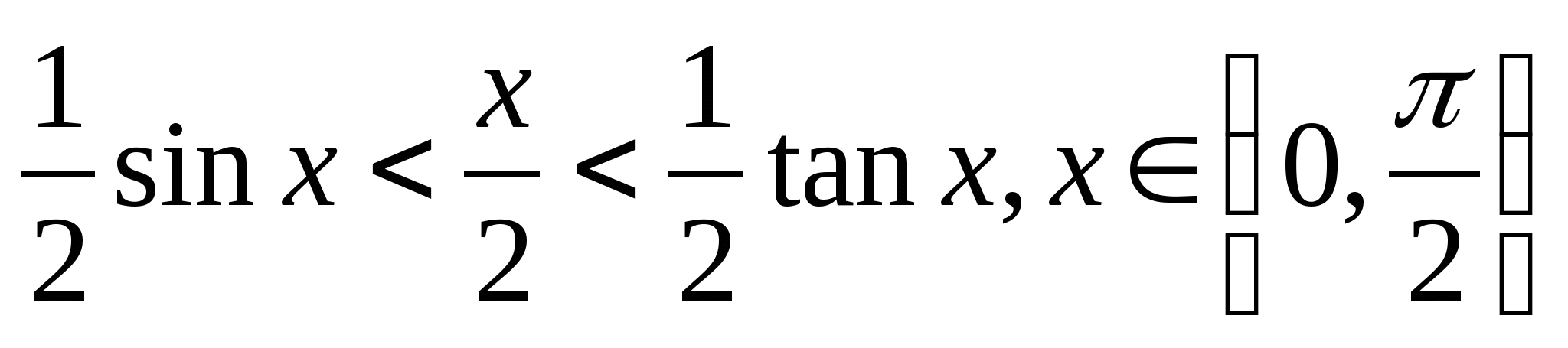
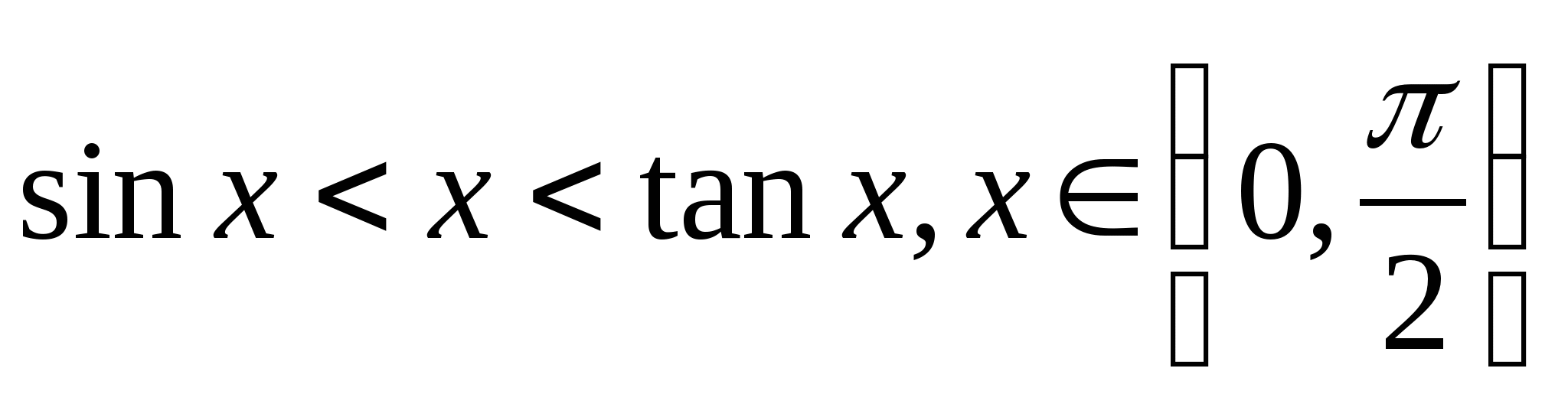
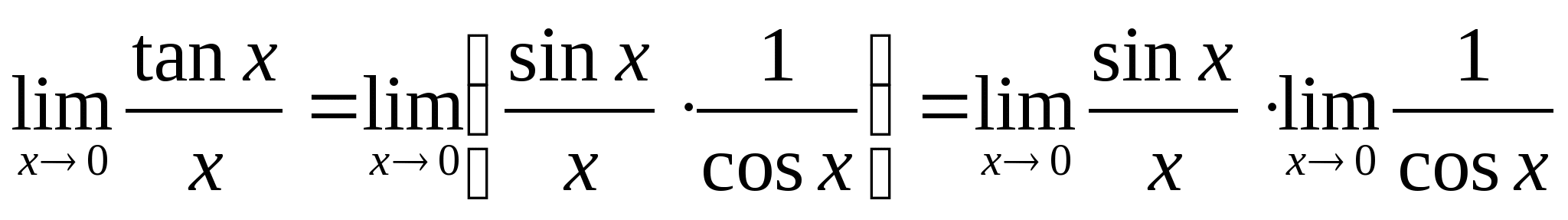
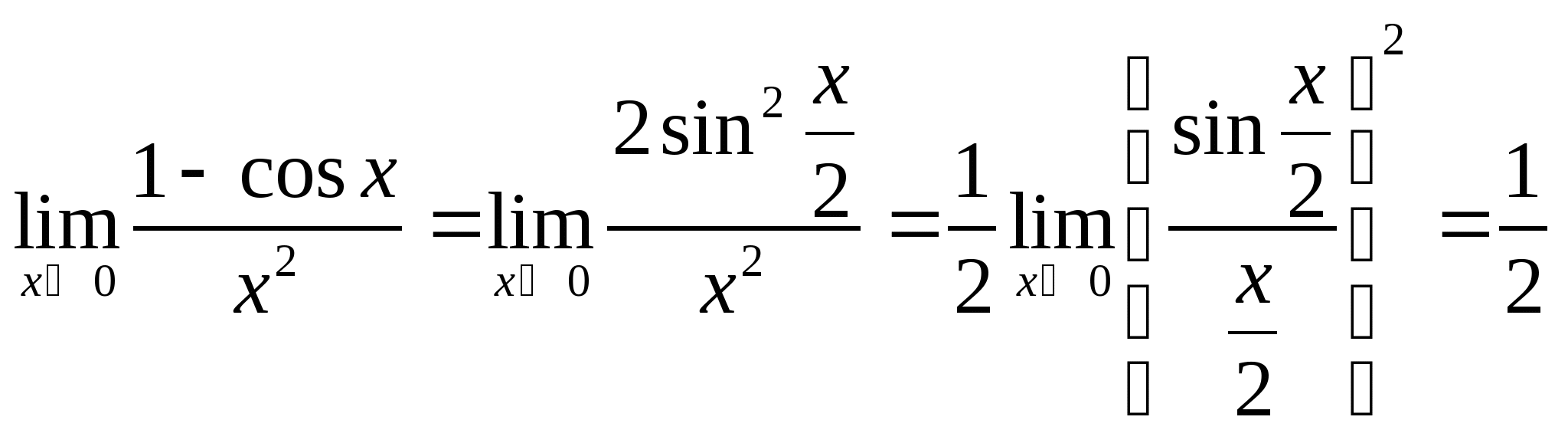
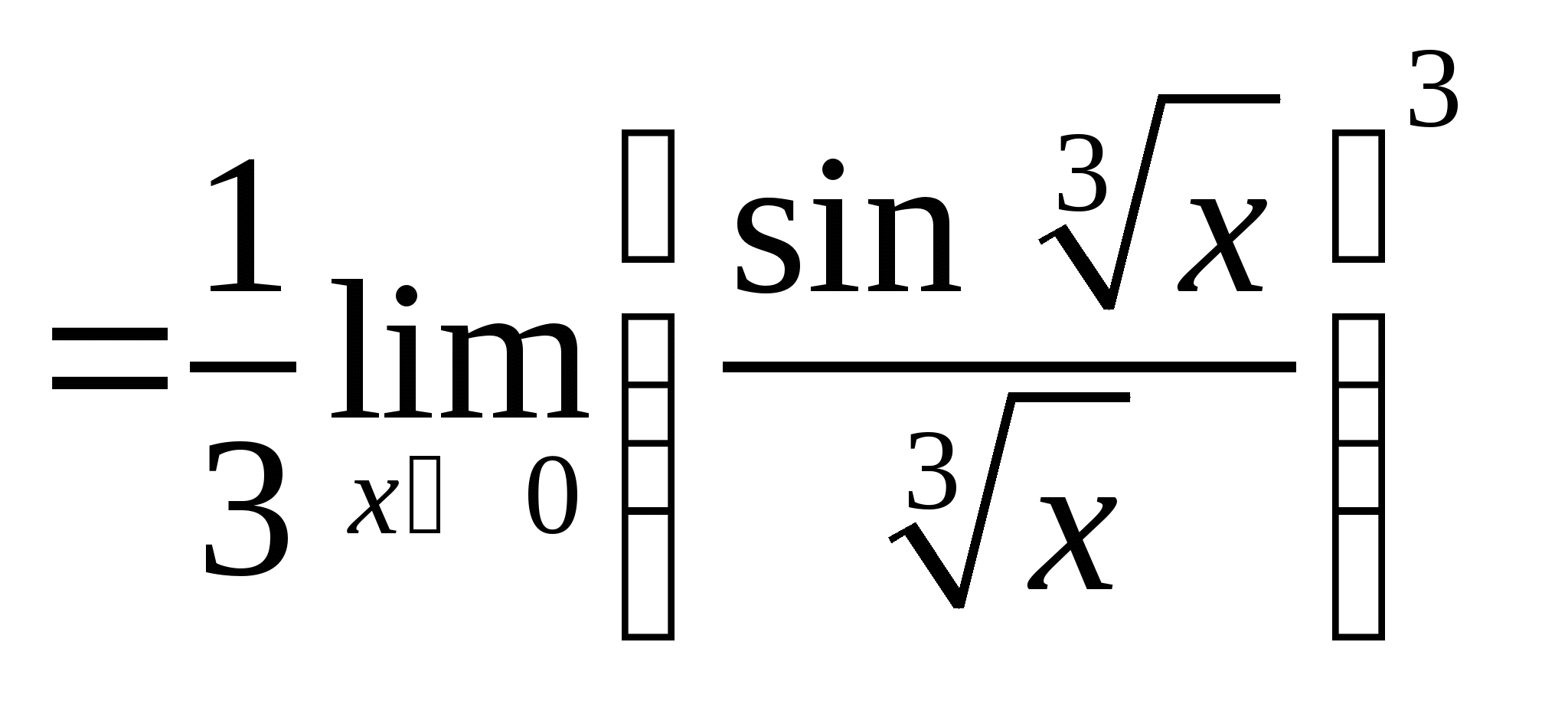
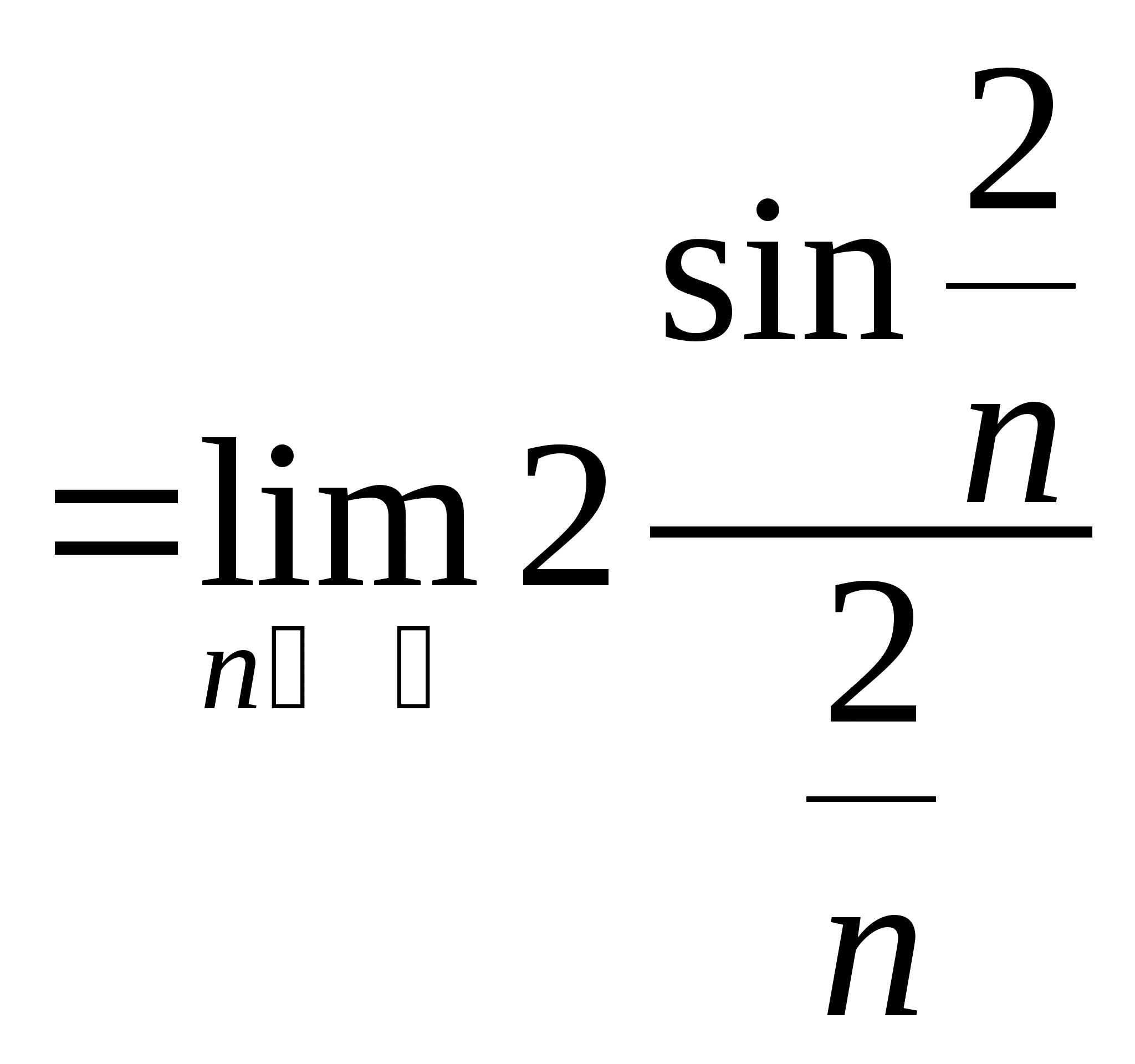
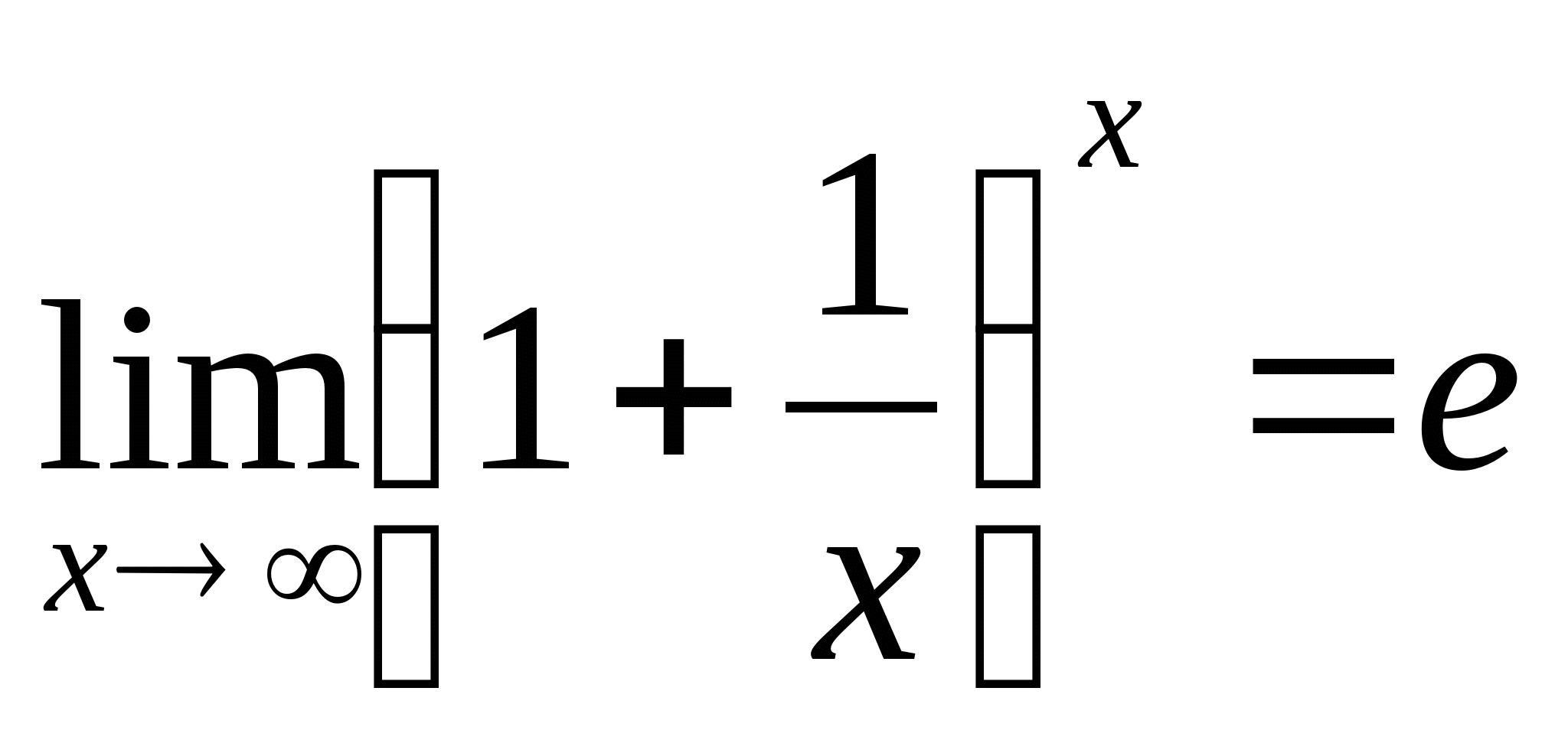
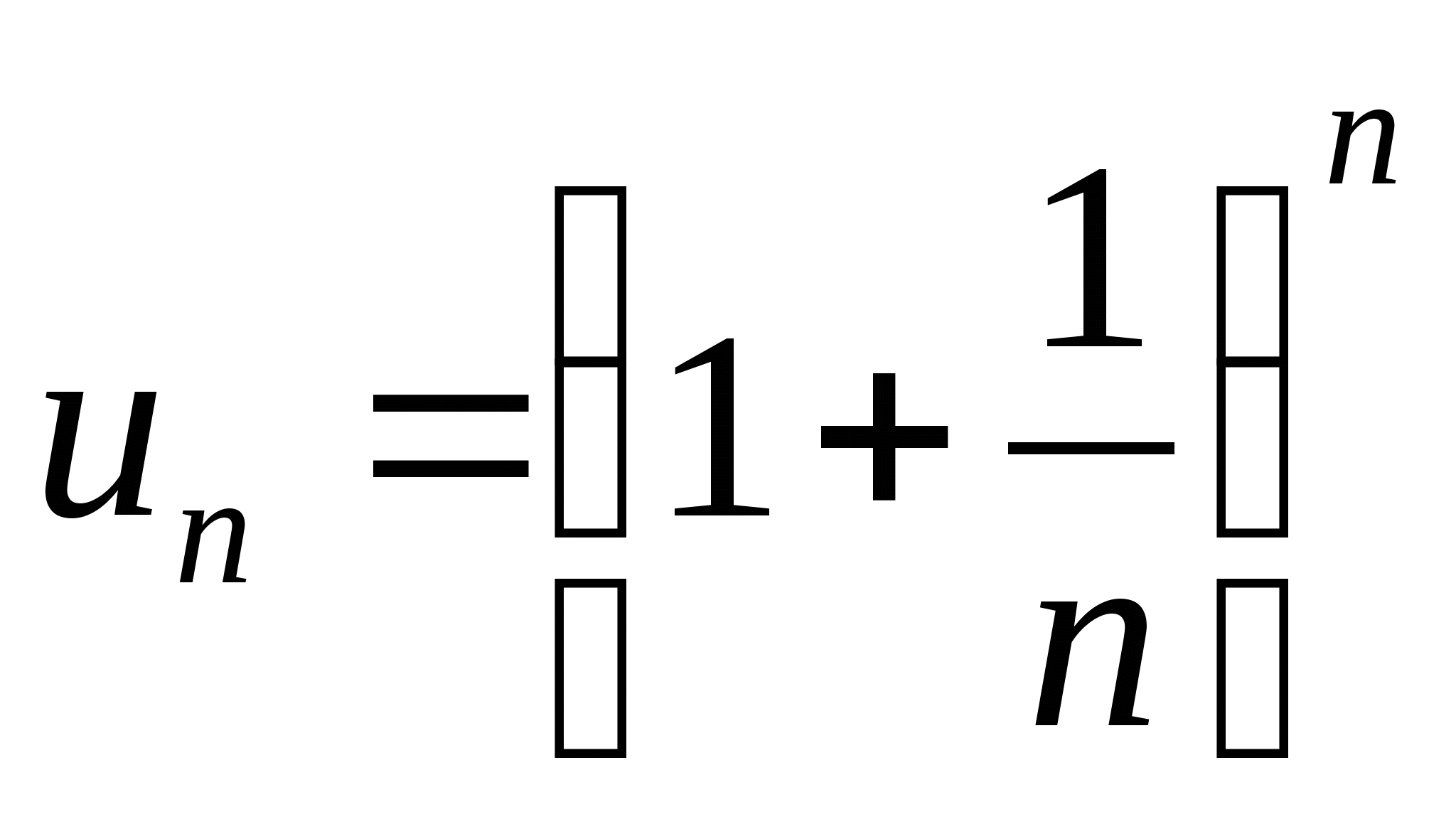 ,由于它单调递增且有界,则它一定收敛,记
,由于它单调递增且有界,则它一定收敛,记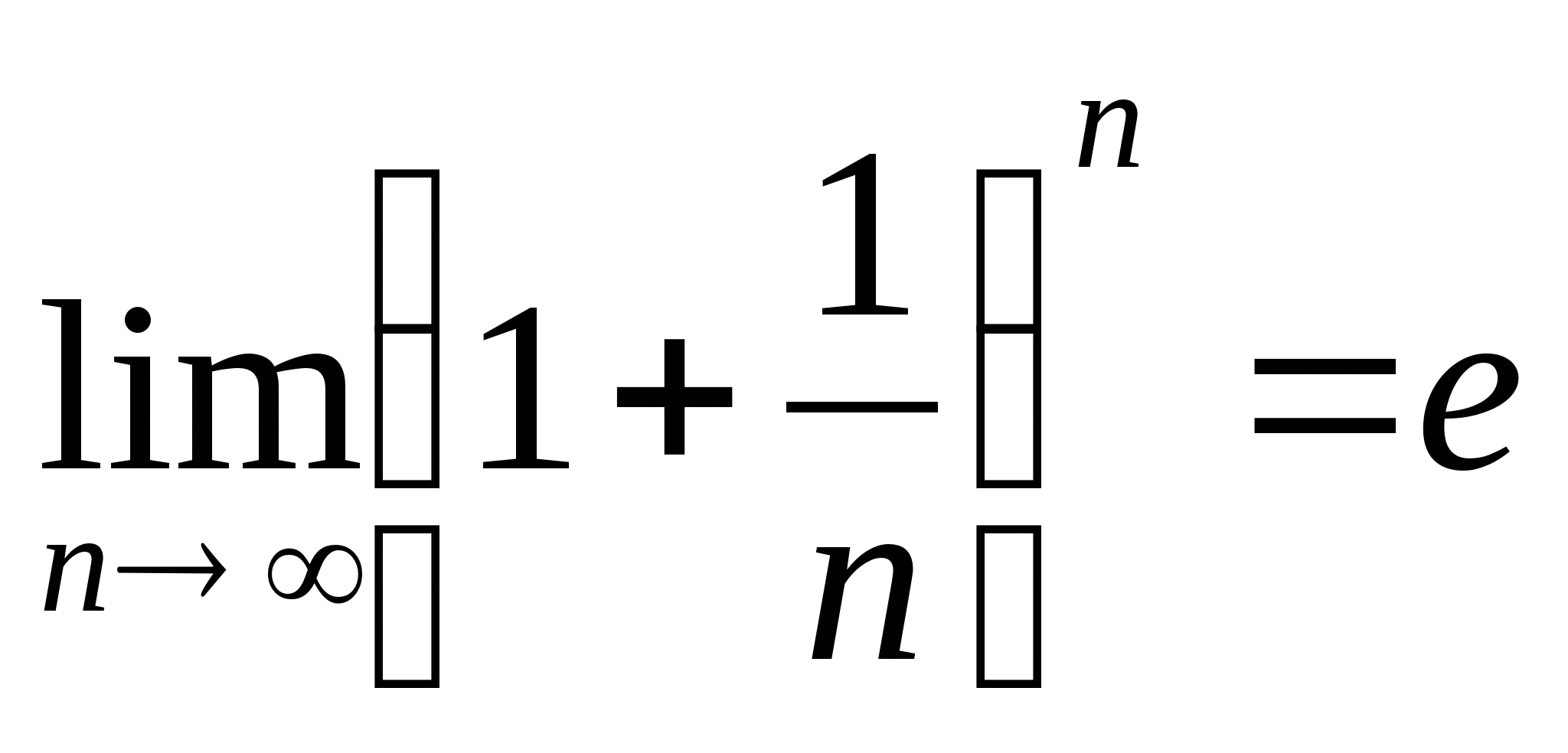
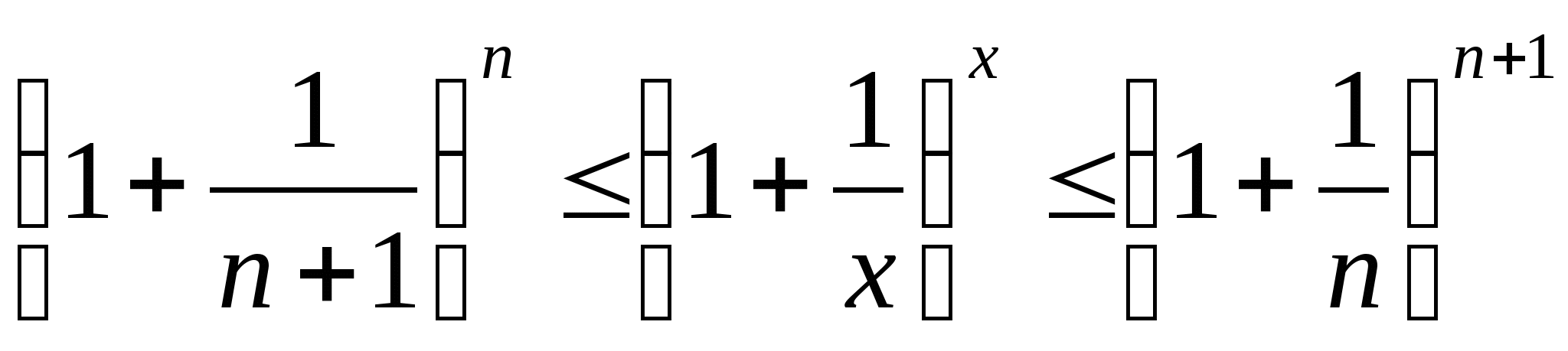
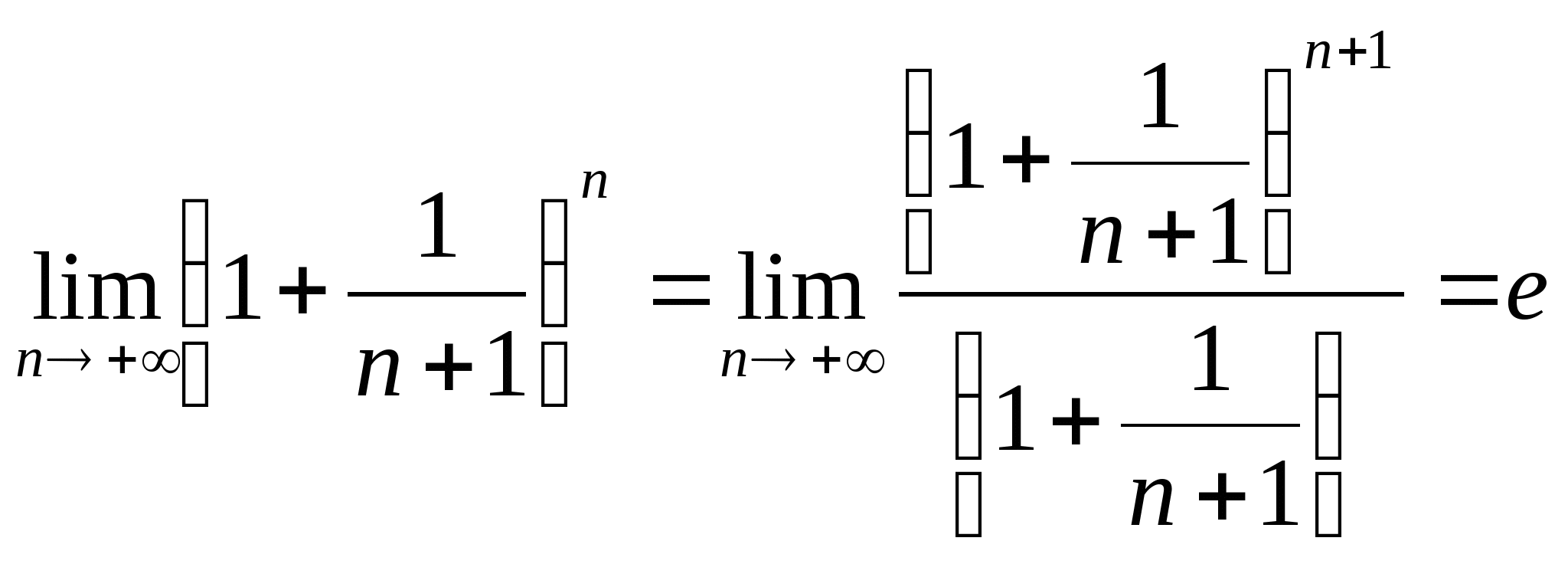
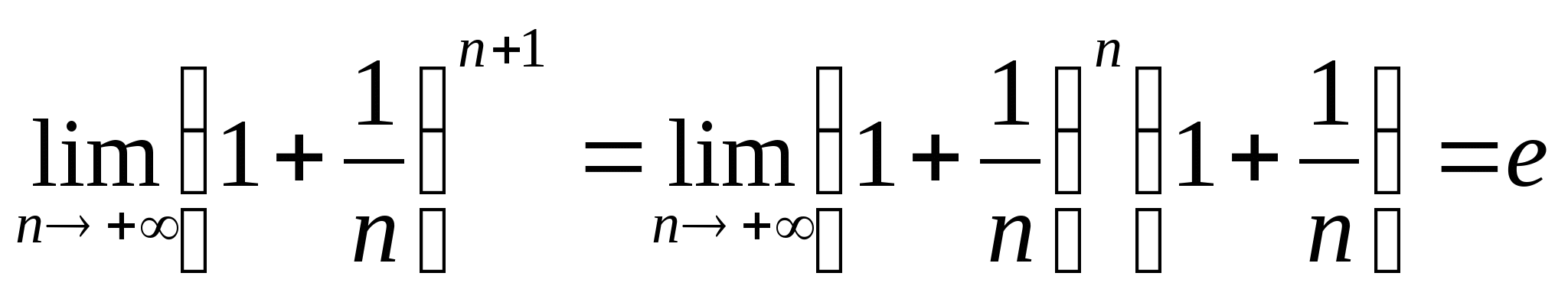
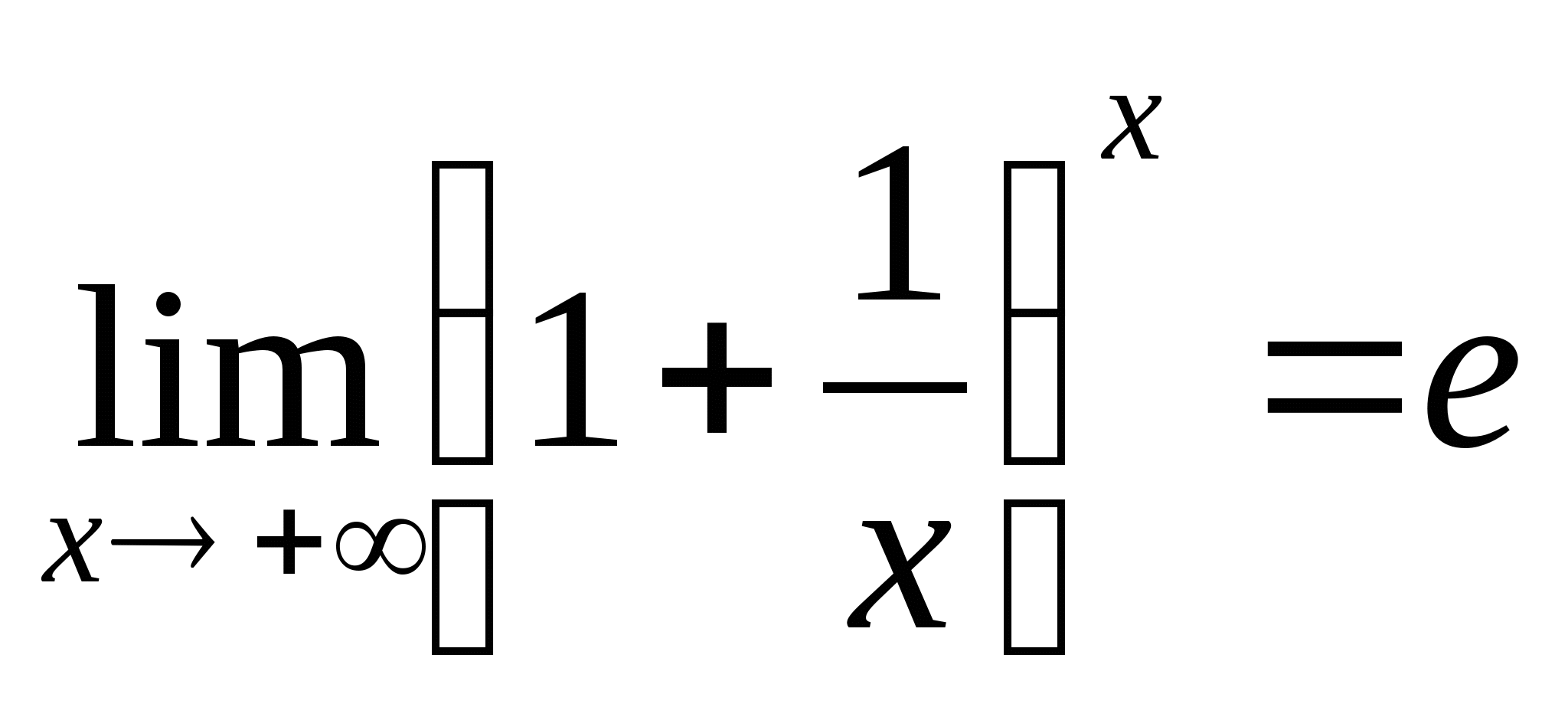
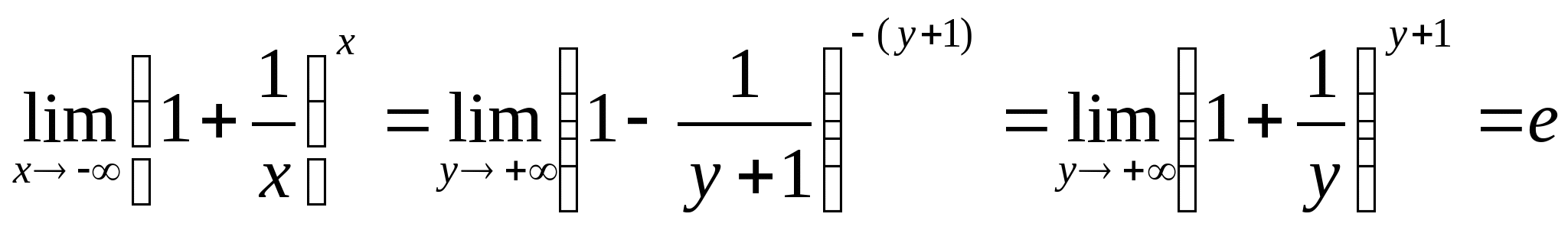
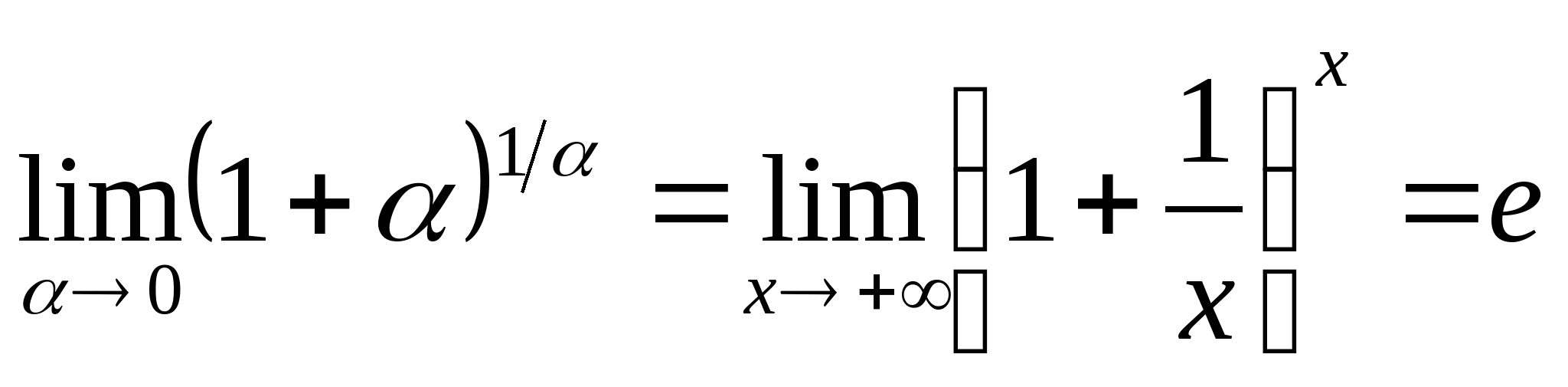
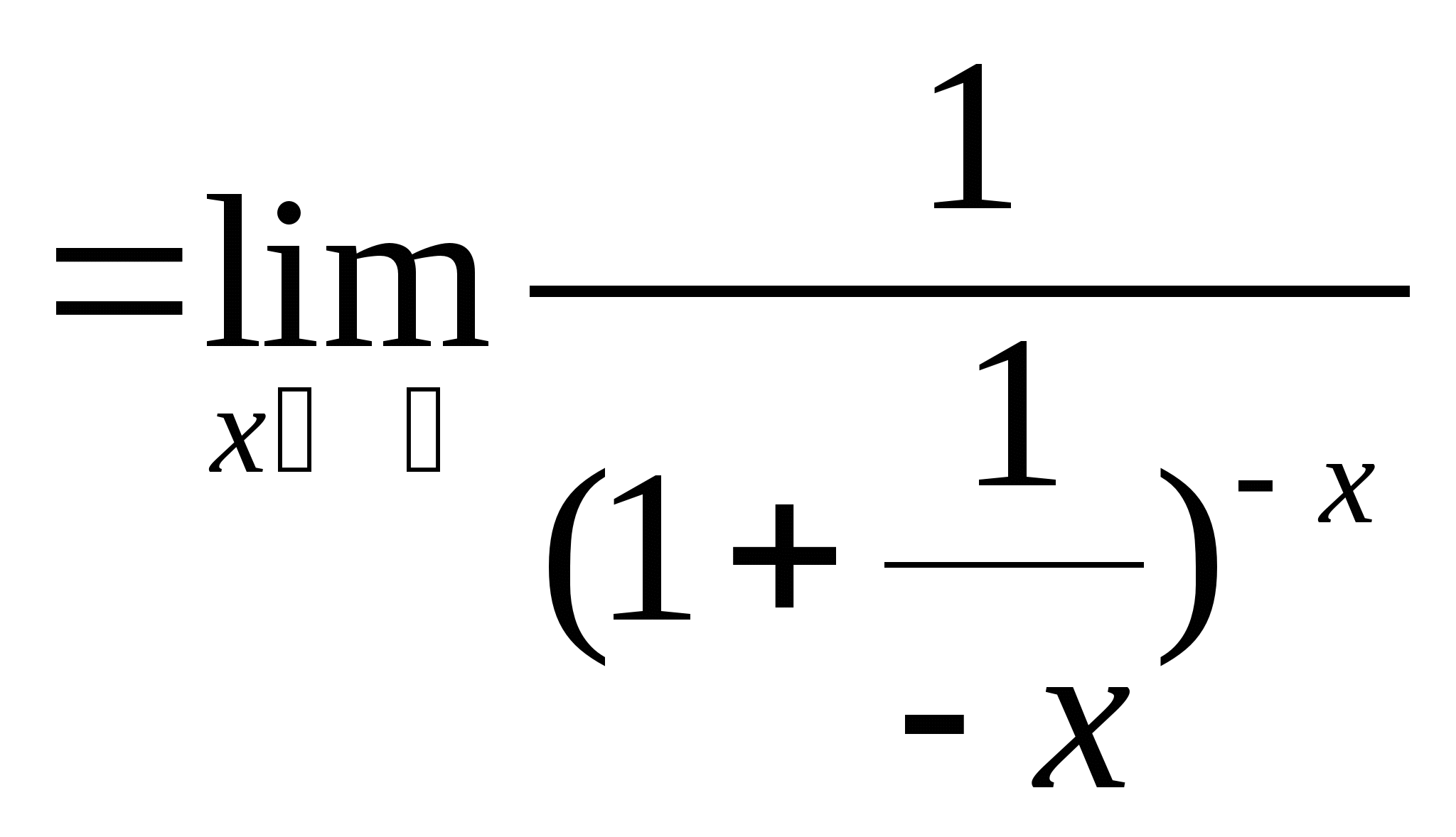
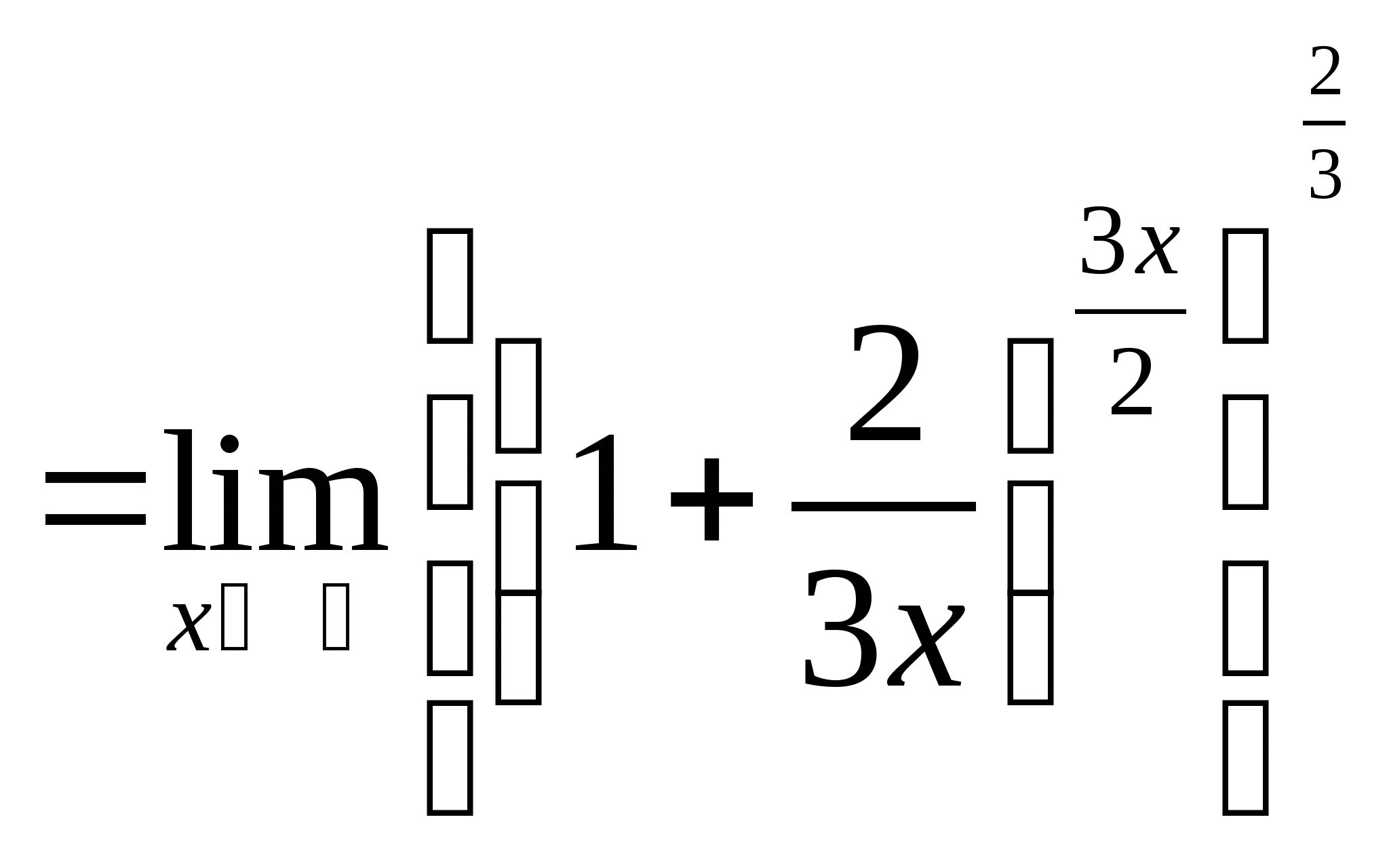
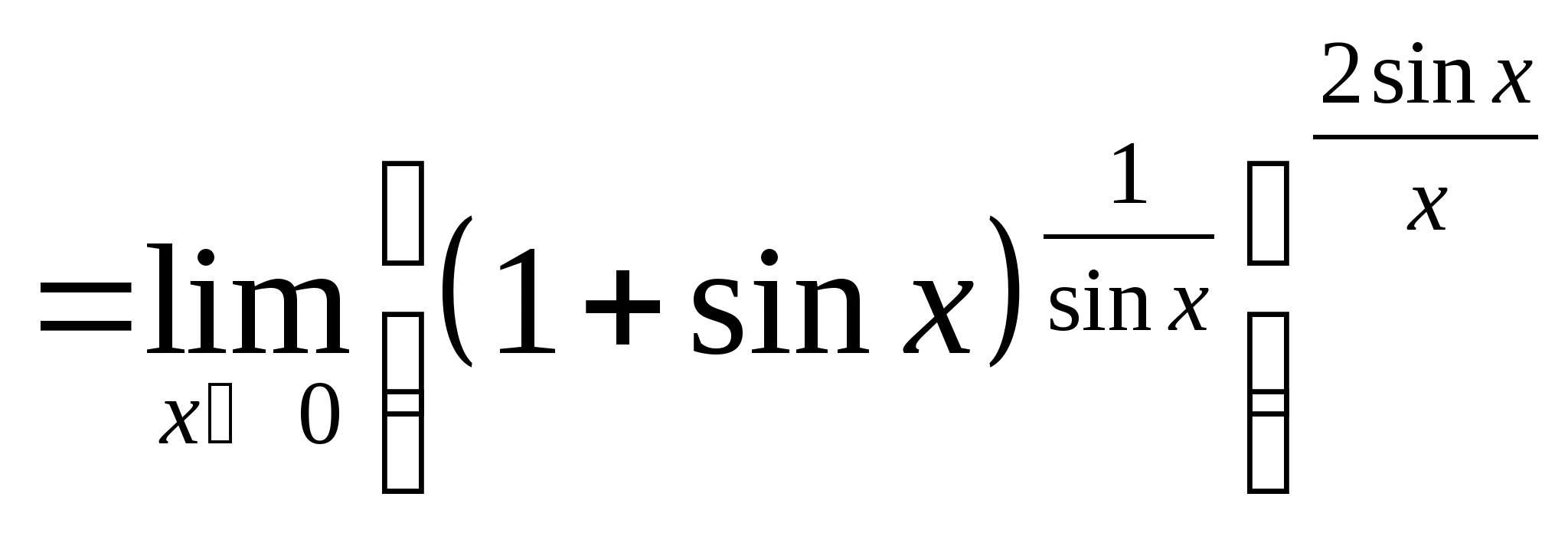
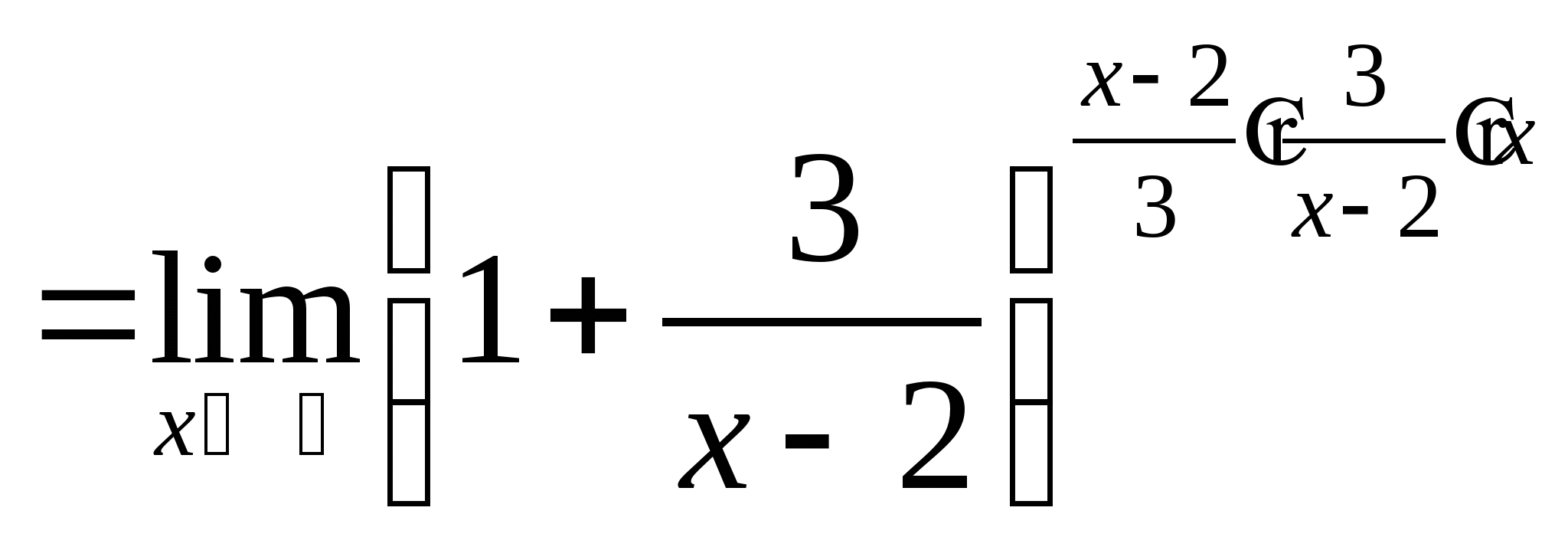 =
=